ist der Geschoßdurchmesser, Ø, in Millimeter. Anfang
von der Nasenspitze bis zum Boden in Kalibern. Anfang
ist die Länge von der Nasenspitze am Bug bis zum zylindrischen Geschoßführungsteil, dem Schaft, in Kalibern. Grundsätzlich bringen schlanke Nasen bei hohen Geschwindigkeiten zu mehreren Mach, Vorteile, also Nasen die mehrer Kaliber lang sind. Erst ab 3 Kalibern Buglänge greifen die widerstandsmindernden Vorteile schlanker Gestalten voll durch. Anfang
[Rt/Rn] = Radius / Tangente / Radius / Nase nennet das Verhältnis zwischen einer tangentialen Ogive und der Nasenogive. Im Riß setzt eine tangentiale Ogive den Schaft im Schaft-Nasen-Übergang fort, schließt also als Tangente glatt an. Eine Sekantogive hingegen knickt am Schaft-Nasen-Übergang vom der koaxialen Schaftriß nach innen ab. Sekanten weisen größere Halbmesser (Radien) als Tangenten auf. Sofern also die Sekante den doppelten Radius wie die Tangente mißt, würde also Rt/Rn 1-fach/2-fach = 0.5 werden. Reine Tangentialogiven werden mit dem Wert 1 eingegeben. Werte über 1 sind unzulässig. Leider sind keine Geschosse günstigsten Wellenwiderstandes bei McCoy mit vorgesehen. vieleich programmiere ich später mal die Haackspitzen als Auswahl mit herein. Robert McCoy kannte entweder Wolfgang Haacks Arbeiten nicht, oder kümmerte sich nicht drum. Anfang
Sofern sich das Geschoß zum Heck hin verjüngt, also das Geschoß achtern wie ein ein Kegelstumpfheck aussieht, gib die Hecklänge in Kalibern ein. Bei einen flachbödigem Geschoß setze den Wert ,,0" ein. Sich verjüngende Hecke verkleinern die Bodenfläche, an denen der Bodensog angreift. Sofern das Heck schlank ist, verursacht die Strömung dort nur wenig Widerstand. Bei langsamen Geschossen ist der Bodensog zu den anderen Widerständen verglichen groß. Bei langsamen Geschossen sind hinter Kegelstumpfhecke also sinnvoll. Bei sehr schnellen Geschossen trägt der Wellenwiderstand der Nase am meisten zum Gesamtwiderstand bei. Anfang
Der Bodendurchmesser betragt bei flachbödigen Geschossen 1 Kaliber. Bei Kegelstumpfheckgeschoßen entsprechend weniger; also trage eine Zahl unter 1 ein. Werte über 1 sind unzulässig. Da der Bodensog bei langsamen Geschwindigkeiten das Geschoß in Luft am meisten bremst, sind hinten schlanke Geschosse für solche Fälle geeignet. Unterschallgeschoße sind im beten Falle wie ein fallender Wassertropfen gestaltet, also vorn rund und hinten schlank, einem Fische ähnlich. Anfang
Oft ist die Nasenspitze nicht ganz spitz, sondern platt mit einer kleinen Kappe angeschlossen. Auch Hohlspitzgeschoße für Wettbewerbe verjüngen sich am Bug nicht in eine Spitze, sondern zeigen eine kleine Platte. Gib den Platten- oder Kappendurchmesser in Kalibern ein. Vollständig spitze Geschosse erhalten den Wert ,,0". Anfang
Sofern das Geschoß feldkalibrig gebaut ist, also nicht der ganze Schaft bis zu den Zügen reicht, und nur ein Führband in die Züge gepreßt wird, um die Leistenkräfte zur Drallerzeugung aufzunehmen, setze den Führbanddurchmesser in Kalibern ein. Gewöhnliche Büchsengeschoße erhalten mangels Führband den Wert ,,1". Granaten mit Führband eine Wert > ,,1". Anfang
McCoy sah die Masse in seinem Programm nicht vor. Hier frage ich die Geschoßmasse dennoch ab um in der Tafel aus Schnelle, Masse, Fläche und Luftwiderstand den Verzögerungsbeiwert auszurechnen, der in der Außenballistik gebraucht wird, um die Flugbahn zu berechnen. Gib die Masse in Gramm ein. Das Programm selbst rechnet im MKS-System. Anfang
Beginne ab diesem Schwellwert die Tafel zu rechnen oder die Graphik zu zeichnen. Tiefe Unterschalwerte zu nehmen, ist wenig sinnvoll, weil die Genauigkeit unter 0,5 Mach schwindet und die Geschosse wie ein Stein vom Himmel fallen, so daß eh kaum noch vernünftig gezielt werden kann. Anfang
Rechne oder zeichne bis zu diesem Ende. Bis 5 Mach liefert das Programm für die üblichen ogivalen Büchsengeschoße genaue Werte inner halb weniger Prozent Abweichung. Anfang
Je nach Größe und Schnelle wird die Luft um das Geschoß eher laminar oder eher turbulent strömen. Ein Maß bietet die Reynold'sche Zahl. Der erste Eintrag ist für den Bug, der zweite für den Schaft. ,, l, l " bedeutet alles strömt laminar; ,, l, t " Bug laminar, Heck turbulent ist voreingestellt und schließlich ,, t, t ": Alles strömt turbulent.
Das Programm stammt von Robert McCoy im US Army Armament Research and Development Command, Ballistic Research Laboratory, Aberdeen Proving Ground, Maryland und wurde 1974 in Basic für den Tandy geschrieben und Februar 1981 als Technical Report ARBRL-TR-02293 veröffentlicht. Der Programmurtext ist hier. Ich übertrug den lediglich in JavaScript. Sollte jemand Fehler finden, möge er die mir bitte mitteilen.
Das Programm ist an die viele Messungen angepaßt und ist innerhalb praktischer Grenzen genau.
Der ballistische Beiwert oder Koeffizient ,,bc“, den ich in der Tafel angebe, gründet sich auf die von Arthur Peijsa vorgeschlagen Umrechnung des Verzögerungsbeiwertes b zu den Mayewski-Tabellen: b = bc*Wurzel(V)*a; Für metrische Rechnung beträgt der Umrechnungsfaktor ,,a0147 etwa 91,65. Ingalls, der Mayewski's Messungen des ausgehenden 19ten Jahrhundertes bei Krupp ins Amerikanische übertrug, benutze 3.600 Fuß / Sekunde als Geschwindigkeitsmaßstab, oder 1097.28 m/s oder bei 20°C 3.189 Mach. Diesen Wert lege ich für die Tafel zugrunde.
Der Sinn eines Luftwiderstandsprogrammes ist aus der Gestalt und Masse, mittels einer Abschußgeschwindigkeit V0 die Flugbahn zu berechnen. Dank dieses und des Außenballistikprogrammes ist das 2002 nun im Netze möglich. Mit Lutz Tautenhahn's JavaScripGrafik für HTML können die Graphen nun auch gleich betrachtet werden. Somit kann mittels Versuch für jede Flugbahnaufgabe aus den Randebedingungen das passende Geschoß mitsamt Mündungsgeschwindigkeit gefunden oder rückgerechnet werden. Dazu trage die geometrischen Geschoßmaße oben ein und drücke dann die Schaltflächen:
Erst wenn du siehst, wie schnell Geschosse in großer Entfernung fallen, wirst du erkennen, wie genau die Entfernung bekannt sein muß, um das Ziel in der Höhe noch zu treffen. Die Programme wurden in dieser leicht benutzbaren Art geschrieben, um die Munition für das weitreichende Scharfschützengewehr zu bestimmen. Dazu muß bei McCoy allerdings noch die Haackspitze mit eingebaut werden, die immerhin schon 1941 beschrieben wurde. Deutschland war den Amerikanern also lange voraus. Theodore von Kármán, der bei Prandtl, dem Vater aller Strömungsmechanik, in Göttingen lernte, fand bereits in den 20er Jahren des vorigen Jahrhunderts eine erste analytische Lösung für Geschosse geringsten Luftwiderstandes, die Haack dann 1941 vervollkommnete.
Wolfgang Haack
Luftwiderstand

Hallo Lutz,
Du meintest am 10.06.02 um 20:00 in einer Mail an mich:
LM > Die Grafiken meiner Luftwiderstandsseite sind sehr speziell
formabhängig.
Ich beschränkte mich ja auch auf die Kugel und auf den *ungefähren* Verlauf der
Kurve (der bei allen ja eine gewisse Ähnlichkeit aufweist).
LM > Ohne die zugrundeliegenden Gedanken, wie sich die Kurven aus der
Impulserhaltung herleiten lassen, ist es ziemlich blauäugig die auf
astronomische Geschwindigkeiten zu übertragen.
Anderen Aussagen in de.sci.physik zufolge gibt es einen Grenzwert für den
cw-Wert, der für steigende Geschwindigkeit angestrebt wird und knapp unter 1
liegt. Erst wenn mean free path in die Größenordnung des Geschoßdurchmessers
kommt, steigt cw auf etwa den doppelten Wert an (für Satelliten wird AFAIK cw=2
angenommen), weil der Vorfaktor 0.5 der
Staudruckformel wegfällt und Stoßgesetze gelten. Für eine Kugel wäre cw=2 bei
elastischem Stoß der Moleküle und cw=4 bei flacher Frontseite.
LM > Als Masseverlust Ansatz würde ich mich mit der Verdampfungswärme von
Meteoritenstoff und dessen Wärmeleitfähigkeit beschäftigen.
Wärmeleitfähigkeit wird vernachlässigbar, da die strukturelle Zerstörung durch
Abdampfen weitaus schneller vonstatten geht. Der Kern des Meteoriten wird nicht
heiß, weil die Wärme zu ihm geleitet wird, sondern weil alles um ihn herum
wegdampft. Und dazu ist eine materialabhängige Arbeit abhängig. Wichtiger ist
vielmehr der (mir leider unbekannte und sehr grob als konstant angenommene)
Anteil der Reibungsarbeit, der zum Abdampfen verbraucht wird. Ca. 10 % gehen m.W.
(bzw. laut Aussagen in
astronomischen Gruppen) durch das Leuchten drauf, ein erheblicher Teil wird
mechanisch an die Luft abgegeben (v.a. Stoßwelle).
LM > Meteoriten verdampfen binnen weniger Sekunden (oder schlagen ein) über
erhebliche Raumwinkel, sprich Strecken, also wohl bis zu hunderten Kilometern,
je nach Einfallswinkel.
Eben, und aus dem Anfängerpraktikum sowie Alltagserfahrung weiß ich, daß ein
Festkörper dieser Größe (cm-Bereich) meist viel länger braucht, um durch
Wärmeleitung gleichmäßig heiß zu werden.
LM > Als Jäger beim Sauansitz sehe ich nacht viel Sternschuppen(Grins) -
wieso eigentlich im Sommer häufiger als im Winter?
mehr klare Nächte (besseres Wetter)
Meteorschwärme (z.B. Perseiden)
LM > Wie errechnest du die Bremsleistung (Bremsarbeit je Zeit) ohne eine
physikalisch vernünftige Staudruckformel zu haben?
Nach div. Aussagen ist die Annahme eines für v>>Mach1 konstantenm cw- Werts um 1
durchaus vernünftig. Der Rest folgt dann aus Energieerhaltung und
Grundgleichungen der Mechanik (hier: dW = F*dx).
Immerhin passen die Ergebnisse gut zu den Tabellen des Massenverlustes sowie
grob zum Helligkeitsprofil von Meteoren. Und zwar egal ob man Sternschnuppen
oder Tunguska-Klasse-Brocken nimmt.
Gruß,
Ingo Thies, Freitag, 14. Juni 2002
Literaturhinweise Außenballistik - Luftwiderstand f. H. Lutz Möller
Barth, H.
Die Normalkraft-, Druckpunkt-, und Tangentialkraftcharakteristiken schlanker Bug- Zylinder-Konfigurationen im Machzahlbereich 0,8 - 4,0
MBB- Ottobrunn 1973, FBWT 73-32
Barth, H.; Hartmann, K.
Druckverteilungsmessungen an einem Rumpf und zwei Flügel-Rumpf Kombinationen zur Untersuchung nichtlinearer Normalkraft und Momentencharakteristiken
MBB GmbH, Ottobrunn 1971, FBWT 1971-24 ,
Damberg, James E.
Numerical Modeling of Rotating Band Flow Field and Comparison wich Experiment Mechanical and Aerospace Engineering Department, Univ. of Delaware
U.S. Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD , 198
MAEP, ein Fortran IV Programm für die Berechnung aerodynamischer Beiwerte von Flugkörpern und für die Aufbereitung von Windkanalergebnissen zu Vergleichszwecken
MBB GmbH, FBWT 74-20
Duncan, Louis D.; Engebos, Bernard F.
A Six-Degree-Of Freedom Digital Computer Program for Trajectory Simulation Atmospheric Sciences Laboratory
White Sands Missile Range, New Mexico ECOM-5158, Oct. 1967
Dwyer, H.A.; Sanders, B.R.
Magnus Forces an Spinning Supersonic Cones - Part 1 and II University of California, Davis , CA
Sandia Laboratories, Livermore, CA
AIAA J., Vo1.13 and 14, 1976
Edmunds, Hans
Aerodynamische Beiwerte und Lage der Bugsto/3welle für Kreiskegel mit spitzer und kugelförmig abgerundeter Nase im Überschall
DFVLR- Köln 1976, DLR-FB-76-26
Esch, H., Hartmann, K., Barth, H.
Drei - Komponenten - Messung im transsonischen Geschwindigkeitsbereich an systematisch variierten Bug-Zylinder - Konfigurationen
MBB GmbH, Ottobrunn 1971, FBWT 1971-23
Esch, H.
Untersuchungen an zwei Modellen von steuerbaren Wiedereintrittsflugkörpern im Transschall- und Überschallbereich
DFVLR 1968, FBWT 1968-68
Esch, H.
Windkanalmessungen an Modellen der Wiedereintrittsflugkörper Erno LBl und LB10
DFVLR 1970, FBW 1970-36
Esch, Helmut
Der Einfluß der Reynoldszahl au f die Normalkraftcharakteristik schlanker zylindrischer Rümpfe
1974, DFVLR FB 75-09
Esch, Helmut
Die 0,6m x 0,6m trisonische Meßstrecke der DFVLR in Köln-Porz Köln 1986
DFVLR Mitt. 86-21
Fleck, V.
Anwendung der Hamiltonschen Quaternionen auf die Bestimmung der Translations- und Rotationsbewegung eines Geschosses
Tech. Bericht
Institute Saint Louis 1978 FBWT 79-1
Giraud, M.
Über den klassischen Stabilitätsfaktor von drallstabilisierten Zylinderkegelgeschossen - Geschoßform P3C
Institute Saint Louis,1976 FBWT 76-18
Gregoriou, Gregor
Ein Rechenprogramm zur Abschätzung von Beiwerten rotations-symmetrischer Rümpfe bei extrem hoher Anstellung
MBB GmbH 1976 FBWT 1976-11
Hartmann, K.
Aerodynamische Untersuchungen an Flugkörpern im transsonischen Geschwindigkeitsbereich
Teil l: Systematische Dreikomponentenmessungen
DFVLR FB-770-67, AVA-FB-7046
Haseltine, William R.
Non-Linear Magnus Moments
US Naval Ordnance Test Station,
China Lake, CA, USA 1985
Jacobson, I.D.
Magnus Characteristics of Arbitrary Rotating Bodies
School of Engineering and Applied Science, University of Virginia
AGARDograph 171, 1973
Kneubuehl, Beat.
Calculation of the Drag Coefficient of Slender Projectiles in Axial Supersonic Flow
Defense Technology Agency, Ballistics Division,
Thun, Switzerland, 1981
Kneubuehl, Beat.; Laube, G.
A Fast Running Solution of the Exterior Ballistics Boundary Value Problem
Defense Technology Agency, Ballistics Division,
Thun, Switzerland, 1981
Legge. H.
Drag Measurements of Cones at Zero Angle of Attack in Near Free Molecular Flow
DLR FB-72-64, Göttingen 1972
Lieske, Robert F.; Reiter, Mary L.
Equations of Motion of a Modified Point Mass Trajectory Model
BRL -Rep. 1314
Aberdeen Proving Ground, Maryland, 1966
Lieske, Robert F.
Use of the Magnus Force in the Modified Point Mass Trajectory Model
BRL-MR-3870
Aberdeen Proving Ground, Maryland, October 1990
Lieske, Robert F; Danberg J.E.
Modified Point Mass Trajectory Simulation for Base-Burn Projectiles BRL-TR-3 3 21
Aberdeen Proving Ground, Maryland, March 1992
Maurer,F.; Niezgodka,J.; Post,H.
Experimentelle Untersuchungen zur Wärmezufuhr im Überschall-Strömungsfeld an Rotationskörpern und an der tangential angeströmten Platte
1970 DFVLR, FB 70-64
Mayer, E.
Ein Programm zur Abschätzung der aerodynamischen Beiwerte und der Geschoßstabilität bei Drallgeschossen
Institute Saint Louis, 1976 FBWT 76-18
McCoy, Robert, L.
A Computer Program for Estimating the Drag Coefficients of Projectiles
U.S. Army Ballistic Research Laboratory, Aberdeen Proving Ground,
MD ARBRL-TR-02293, 1981
Miller, Donald G.
Ballistics Tables for Spheres 7.5 to 25 mm in Diameter
Lawrence Livermore Laboratory, U.S. Department of Energy,
Contract Number W-7405-ENG-48, Jan.1979
Molitz H., Strobel R. Äußere Ballistik
Springer Verlag, 1963, Berlin, Heidelberg
Ostapenko, N.A.; Yakunina, G.Ye.
The Dynamics of Slender Bodies in Dense Media under Conditions of the Local Interaction Model
Moskow 1995
J. Appl. Maths Mechs, Vo1.61, No.6., 1997
Platou, Anders S.
Magnus Characteristics of Finned and Nonfinned Projectiles Ballistic Research Labs., Aberdeen Proving Ground, Md.
AIAA Journal, Jan. 1965
Riedel, Hansgeorg; Edmunds, Hans; Niezgodka, Franz-Joachim
Einfluß der Dickenrücklage und der Rumpflänge von achsensymmetrischen Flugkörpern au f die aerodynamischen Beiwerte im Überschall
1970, DFVLR Forschungsbericht 70-54
Schmieder. L.
Optimale Ausrichtung von rotationsymmetrischen und drallstabilisierten Körpern in Abhängigkeit vom Trägheitsmomentenverhältnis
Raumfahrtforschung Mai 1970
DFVLR Sonderdruck Nr.50
Schmidt, W.R., Herpfner, E.
Zusammenstellung experimenteller Unterlagen zum Heckwiderstand von Flugkörpern im Transschall- und im Überschallbereich und Vergleich mit theoretischen Berechnungsmethoden
Dornier Friedrichshafen, 1973 FBWT 73
Sedney, R.
Review of Base Drag
US Ballistic Research Lab., Aberdeen Proving Ground, 1966
Sells, Ray
Missile Six-Degree-of Freedom Simulation Development
US-ASSDC, Kinetic Energy Weapon Digital Emulation Center,
Teledyne Brown Engineering, Huntsville, AL, 1997
Sturek, W.B.; Mylin, D.C.
Computational Parametric Study of the Magnus Effect an Boattailed Shell
US. Army, BRL, Aberdeen Proving Ground, MD., 1981
6th Int. Symposium an Ballistics, Orlando, FL
Tanner, Mauri
Empirische Formeln zur Bestimmung des Basisdruckes von Flugkörperrümpfen bei Unterschallgeschwindigkeit
FB DFVLR 84-2 3
US-ASSDC An Ada-Based Source Code Environment for Six-Degree-of Freedom (6-DOF) Missile Simulations
US-Army Space and Strategic Defense Command Battlefield Integration Center , Kinetic Energy Weapon Digital Emulation Center (KDEC)
1993-97
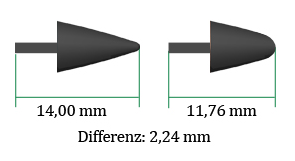
Bild: Waldmann
Hallo Herr Möller
Lässt sich berechnen, um wieviel der BC der runden Kappen abnimmt?
Mit freundlichen Grüßen, Christian Waldmann, Montag, 11. April 2011 09:57