Drag Coefficient

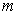Projectile Mass

Air Density

Projectile Reference Area

= Bullet Velocity

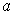= Bullet Acceleration

Muzzle velocity

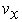lateral Bullet velocity

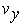forward Bullet velocity

vx

lateral Bullet velocity

ax

lateral Bullet acceleration

forward Bullet acceleration

lateral Wind

forward Wind

is the Projectile Forward velocity (Ballistic wind) and Crosswind combined Airflow.

is the total Projectile drag force.

Since F = m · a, the Bullet accelerates

Let

, so that simplified

, or

Now assume

and

, then

When

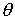is the Lateral wind to Bullet forward velocity Angle,

then

As

and

the lateral acceleration is

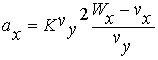or

(1)

Similarly for small

the forward acceleration is

The Minus sign means, the Bullet slows.

The Velocity time differential is Acceleration. So integrating

yields the Velocity.

So

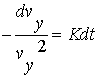integrated gives

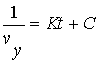At

,

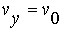so

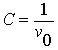the forward velocity becomes

(2)

Similarly, to find the lateral velocity, we integrate the lateral acceleration

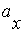from (1)

so substituting

for (1) we get

Rearranging the terms yields

Integrate both Sides to

At

,

so

giving

or

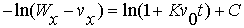By rearranging, the lateral velocity is

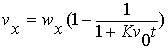(3)

---

We now need the Time for the Bullet to reach the Downrange distance

and so from (2)

integrated gives

At

, so

thus

and

therefore

(4)

Substituting (4) in (3) for

leads to

and integrating gives

(5)

So from (4),

or

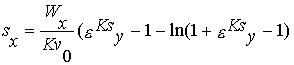then

(6)

Remembering

for the lateral Movement or Deflection we thus have an expression in Drag coefficient terms.

While equation (6) is not intuitive, it clearly shows the Deflection behaves to Muzzle velocity inversely proportional.

To rewrite (6) as

and substitute (4) leads to the Didion Equation

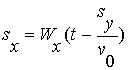The term

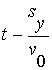is the Difference between Flight time in Vacuum and actual Flight time, or the "Lag" time.

Hence is Didion's Approximation called the "Delay Lag Theory". Given only the Drag coefficient and bullet dimensions, Deflection cannot directly be calculated. However, if the actual Flight time can be measured or calculated, then to calculate the Wind deflection is quite simple.

Mr. Moeller,

Wonderful! Thank you for publishing the Didion Approximation for Wind drift article! as a novice target shooting enthusiast, I've long suspected the existence of the conditions described in the paper, but never had a good mathematical handle on them. I very much appreciate seeing the sound and straight forward treatment of wind drift modeling given in the approximation. Thank you again!

FYI: I first downloaded the .doc version which contains a small error as follows: the second equation describes the total drag force on the projectile, which is then divided by the mass of the projectile to obtain the third equation describing the acceleration (deceleration) of the projectile. In that expression for acceleration, the coefficient of drag is missing. The same error appears in the.php version of the same article. As a minor comment, English readers are accustomed to seeing the character "e", as is used in the article, rather than the Greek character epsilon, to represent the natural base. Anyone with a mathematical background will certainly understand the article, however, and epsilon vs. "e" is not a flaw.

Best regards,

Bob Porter, Sonntag, 13. April 2003 07:00

Lutz Möller